On-sky and hardware rotation angles.#
Abstract
The rotation angles RotTelPos and RotSkyPos are precisely defined
and conversion routines are established.
Introduction#
The Rubin observatory Simonyi Survey Telescope (SST) employs a camera rotator
both to track the sky on its alt-az mount and to facilitate rotational dithering
during survey operations. Two principle rotation angles are used to describe the
orientation of the camera in different engineering and scientific contexts:
RotSkyPos, which orients the projected focal plane with respect to the
celestial sphere, and RotTelPos which orients the physical camera hardware
with respect to the telescope mount assembly (TMA). This document describes the
relationship between these two angles and provides a Python routine to convert
between them.
Definitions#
Optical Coordinate System (OCS)#
See https://sitcomtn-003.lsst.io/#the-optical-coordinate-system.
When the telescope is pointed towards the horizon:
\(+Z_\mathrm{OCS}\) points from M1 towards the camera
\(+Y_\mathrm{OCS}\) points to zenith
\(+X_\mathrm{OCS}\) completes the right-handed coordinate system. It points towards the right as you look from the sky towards the reflective surface of M1.
Addtionally, the OCS origin is the hypothetical vertex of M1, and the OCS follows the TMA as it tracks and slews across the sky.

Fig. 1 Josh in front of TMA with OCS axes indicated.#
Camera Coordinate System (CCS)#
See https://sitcomtn-003.lsst.io/#lsstcam.
Summary:
When
RotTelPosis 0, the CCS is parallel to the OCS.The CCS origin is the vertex of L1S1.
The CCS follows the camera, and rotates with the camera when the rotator is engaged.
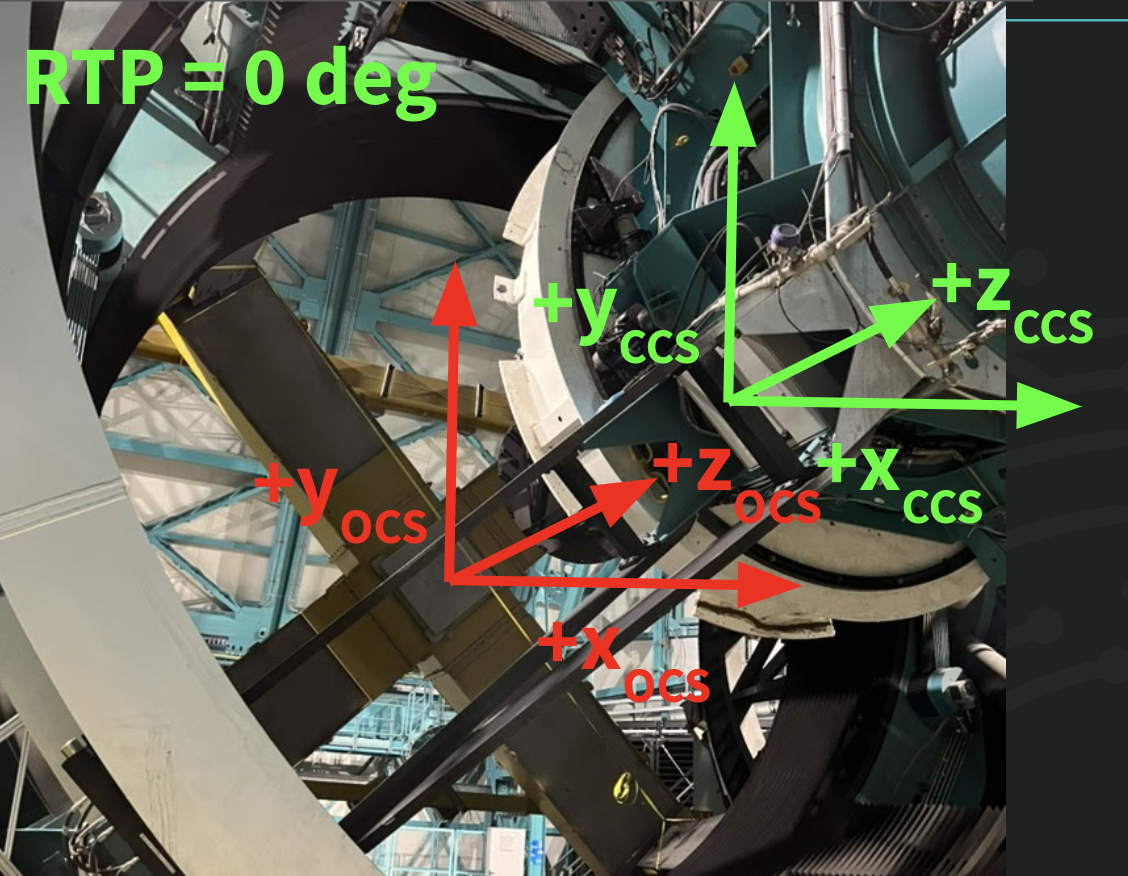
Fig. 2 View from front of TMA, looking towards M1M3 mass surrogate (the large
yellow X), with M2 surrogate and ComCam in the top right of the image.
Camera Coordinate System when RotTelPos = 0 is indicated. (+Z_CCS is
partially out-of-the-page.)#
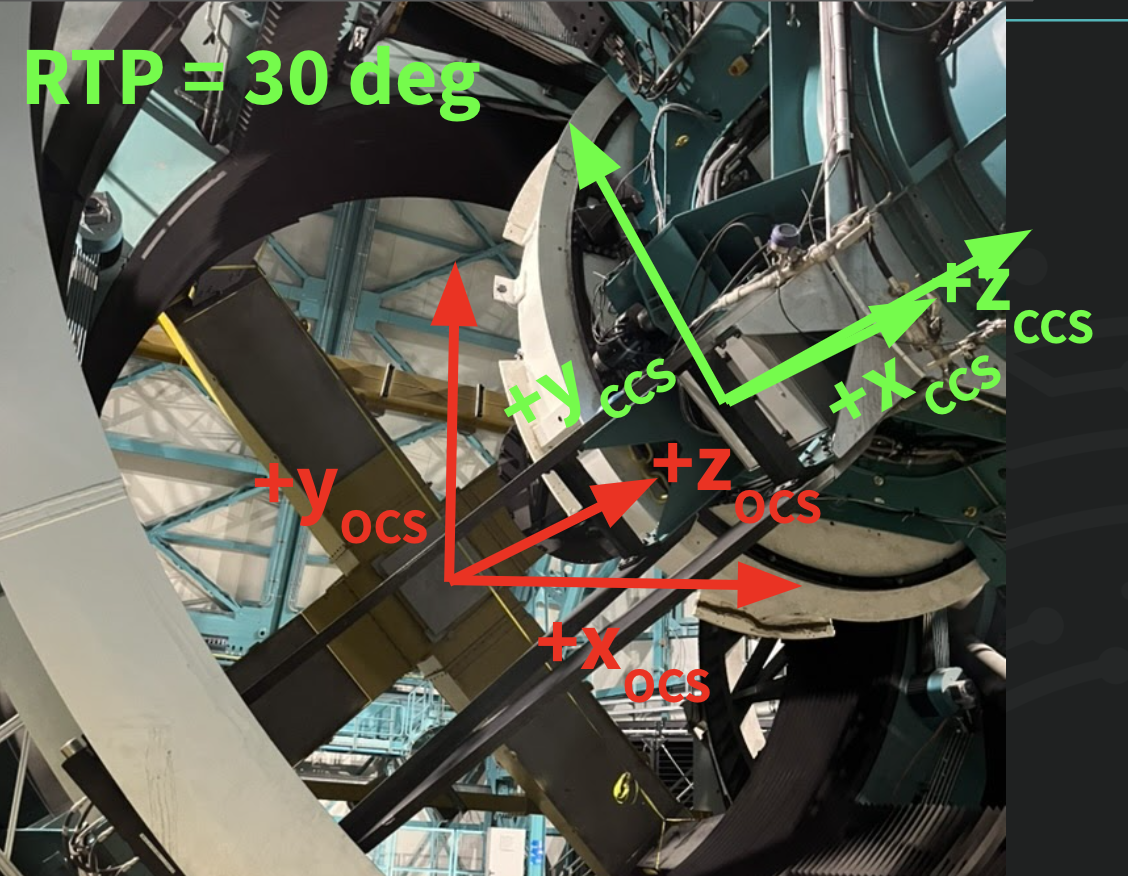
Fig. 3 Same as Fig 2, but indicating RotTelPos = 30
degrees. When viewed from the sky towards M1M3, the camera rotates counter
clockwise with increasing RotTelPos.#
Data Visualization Coordinate System (DVCS)#
The DVCS is the primary focal plane coordinate system used by data management. It is defined as the transpose of the CCS. See https://ls.st/LSE-349 for more details.

Fig. 4 LSSTCam in the clean room with CCS and DVCS axes indicated. RotTelPos
here is 0 degrees.#

Fig. 5 The camera turns clockwise from this point of view as RotTelPos
increases.#
Note how you can infer the camera orientation from the differing layouts and colors of the ITL and e2v CCDs (\(+X_\mathrm{CCS}\) is to the left, \(+Y_\mathrm{CCS}\) is to the top).

Fig. 6 Camera Raft layout. Dark blue rafts are e2v CCDs, light blue rafts are ITL CCDs.#
Raft R24 lies along \(+Y_\mathrm{CCS}\), and R42 along \(+X_\mathrm{CCS}\).
RotTelPos#
This is the camera hardware rotator angle.
When the camera is mounted on the telescope and the telescope is pointed to the horizon, a value of RotTelPos=0 orients the camera such that the \(+Y_\mathrm{CCS}\) points towards zenith.
A positive value of RotTelPos rotates the camera clockwise as viewed from M1M3 towards the camera.
The range of
RotTelPosis limited to -90 degrees to +90 degrees.
RotSkyPos#
This is the orientation of the \(+Y_\mathrm{DVCS}\) axis (projected on the sky) measured east of north in the International Celestial Reference Frame (ICRF).
Parallactic Angle#
This is the position angle (measured east from true North) of zenith at a given sky coordinate.
Note that the definition references true North, which is slightly different from ICRF North, and slowly precessing with Earth’s axis.
When converting between
RotTelPosandRotSkyPos, we require the position angle of zenith measured east from ICRF North.
Pseudo Parallactic Angle#
The position angle (measured east from ICRF North) of zenith at a given sky coordinate.
I don’t know of an official label for this angle. I’m defining it as the pseudo parallactic angle here.
Converting from RotTelPos to RotSkyPos#
Let’s work out an example taking into account the various definitions above. For the moment, we’ll just focus on getting signs right.
Imagine pointing just above the ICRF South Celestial Pole. For concreteness we’ll target HD116244 at sunset on Vera Rubin’s 100th birthday:
ra_ICRF = 13:25:5.13
dec_ICRF = -74:53:32.6
MJD = 61975.91735
Here’s the view from Stellarium:
Fig. 7 HD116244. We’re observing just above the South Celestial Pole (the convergence of blue lines indicates the (true) SCP). At the position of HD116244, zenith is “up”, north is “up”, east is “left”.#
From here, the direction to zenith and the direction to the North Celestial Pole are almost the same. I.e., the parallactic and pseudo parallactic angles are both nearly 0.
Let’s say that RotTelPos = 0 degrees. Then Fig. 6 shows us that R24 is
physically “up” inside the camera, in the sense that it is farther from the
center of the Earth than R20. However, as a consequence of the odd number of
mirrors in the Simonyi Survey Telescope, when projected onto the sky, the
image is rotated 180 degrees! (Or equivalently, reflected through the
origin). R20 is projected towards the top of Fig. 7, and R24 towards the
bottom. Similarly, R42, which lies along \(+Y_\mathrm{DVCS}\), is
projected towards the right of the Fig. 7. Since RotSkyPos is the
orientation of \(+Y_\mathrm{DVCS}\) (“right”) measured east (“left”) of
north (“up”), we can see that it’s about +270 degrees here.
Recall that increasing RotTelPos rotates the camera clockwise when viewed
from M1M3. I.e., R42 rotates towards R43, which must still be true when both
are projected onto the sky. Since the projection onto the sky is also just a
rotation, we conclude that increasing RotTelPos rotates the projection of
the camera clockwise on the sky. If we set RotTelPos = 45 degrees, that
makes \(+Y_\mathrm{DVCS}\) rotate from “right” to “top right”, and we see
that RotSkyPos = +225 degrees. So increasing RotTelPos results in
decreasing RotSkyPos.
Finally, imagine observing HD116244 a few hours later, for concreteness at
MJD = 61976.03248
Here’s the new view from Stellarium:
Fig. 8 HD116244 a few hours later. The Zenith is still “up”, but now the South Celestial Pole is in the lower left. At the position of HD116244, north is “up and right”, east is “up and left”.#
Since the parallactic angle is the direction of zenith from north through east, we can eyeball it at about +45 degrees.
As before, setting RotTelPos = 0 degrees places the projection of R42 (i.e.,
the projection of \(+Y_\mathrm{DVCS}\)) towards the right. We can now
eyeball the value of RotSkyPos as the angle from north (“up and right”)
through east (“up and left”) of \(+Y_\mathrm{DVCS}\) (“right”), about +315
degrees. So increasing the parallactic angle at fixed RotTelPos increases
RotSkyPos.
Combining the above, and using \(q\) for the (pseudo) parallactic angle, we arrive at the relation:
The final wrinkle is that we’d like our definition of RotSkyPos to reference
ICRF north and not true north. This means that for precise results we need to
use the pseudo parallactic angle. Unfortunately, this value isn’t readily
available in most astrometry libraries. We provide a routine to compute it
directly below.
Code#
The following code can be used to transform between RotSkyPos and
RotTelPos. We use the precise relation that uses the pseudo parallactic
angle. We’ve also added interfaces for setting the ambient pressure,
temperature, relative humidity, observation wavelength, and observatory
coordinates.
Note that like all astrometric computations, results can be sensitive to which Earth ellipsoid, precession and nutation models you use.
import astropy.units as u
from astropy.coordinates import AltAz, Angle, EarthLocation, SkyCoord
from astropy.time import Time
def pseudo_parallactic_angle(
ra: float,
dec: float,
mjd: float,
lon: float = -70.7494,
lat: float = -30.2444,
height: float = 2650.0,
pressure: float = 750.0,
temperature: float = 11.5,
relative_humidity: float = 0.4,
obswl: float = 1.0,
):
"""Compute the pseudo parallactic angle.
The (traditional) parallactic angle is the angle zenith - coord - NCP
where NCP is the true-of-date north celestial pole. This function instead
computes zenith - coord - NCP_ICRF where NCP_ICRF is the north celestial
pole in the International Celestial Reference Frame.
Parameters
----------
ra, dec : float
ICRF coordinates in degrees.
mjd : float
Modified Julian Date.
latitude, longitude : float
Geodetic coordinates of observer in degrees.
height : float
Height of observer above reference ellipsoid in meters.
pressure : float
Atmospheric pressure in millibars.
temperature : float
Atmospheric temperature in degrees Celsius.
relative_humidity : float
obswl : float
Observation wavelength in microns.
Returns
-------
ppa : float
The pseudo parallactic angle in degrees.
"""
obstime = Time(mjd, format="mjd", scale="tai")
location = EarthLocation.from_geodetic(
lon=lon * u.deg,
lat=lat * u.deg,
height=height * u.m,
ellipsoid="WGS84", # For concreteness
)
coord_kwargs = dict(
obstime=obstime,
location=location,
pressure=pressure * u.mbar,
temperature=temperature * u.deg_C,
relative_humidity=relative_humidity,
obswl=obswl * u.micron,
)
coord = SkyCoord(ra * u.deg, dec * u.deg, **coord_kwargs)
towards_zenith = SkyCoord(
alt=coord.altaz.alt + 10 * u.arcsec,
az=coord.altaz.az,
frame=AltAz,
**coord_kwargs
)
towards_north = SkyCoord(
ra=coord.icrs.ra, dec=coord.icrs.dec + 10 * u.arcsec, **coord_kwargs
)
ppa = coord.position_angle(towards_zenith) - coord.position_angle(towards_north)
return ppa.wrap_at(180 * u.deg).deg
def rtp_to_rsp(rotTelPos: float, ra: float, dec: float, mjd: float, **kwargs: dict):
"""Convert RotTelPos -> RotSkyPos.
Parameters
----------
rotTelPos : float
Camera rotation angle in degrees.
ra, dec : float
ICRF coordinates in degrees.
mjd : float
Modified Julian Date.
**kwargs : dict
Other keyword arguments to pass to pseudo_parallactic_angle. Defaults
are generally appropriate for Rubin Observatory.
Returns
-------
rsp : float
RotSkyPos in degrees.
"""
q = pseudo_parallactic_angle(ra, dec, mjd, **kwargs)
return Angle((270 - rotTelPos + q)*u.deg).wrap_at(180 * u.deg).deg
def rsp_to_rtp(rotSkyPos: float, ra: float, dec: float, mjd: float, **kwargs: dict):
"""Convert RotTelPos -> RotSkyPos.
Parameters
----------
rotSkyPos : float
Sky rotation angle in degrees.
ra, dec : float
ICRF coordinates in degrees.
mjd : float
Modified Julian Date.
**kwargs : dict
Other keyword arguments to pass to pseudo_parallactic_angle. Defaults
are generally appropriate for Rubin Observatory.
Returns
-------
rsp : float
RotSkyPos in degrees.
"""
q = pseudo_parallactic_angle(ra, dec, mjd, **kwargs)
return Angle((270 - rotSkyPos + q)*u.deg).wrap_at(180 * u.deg).deg
Finishing the example#
Here’s our example coded up:
import warnings
from astropy.utils.exceptions import AstropyWarning
with warnings.catch_warnings():
warnings.simplefilter('ignore', AstropyWarning)
ra = Angle("13h25m05.13s").deg
dec = Angle("-74d53m32.5s").deg
mjd = 61975.91735
print("pseudo parallactic angle")
print(pseudo_parallactic_angle(ra, dec, mjd), " deg")
print("expect ~0 deg")
print()
# Check astroplan parallactic angle
from astroplan import Observer
coord = SkyCoord(ra*u.deg, dec*u.deg)
observer= Observer.at_site("LSST")
obstime = Time(mjd, format='mjd', scale='tai')
print("parallactic angle from astroplan")
print(observer.parallactic_angle(obstime, coord).deg, " deg")
print("expect ~0 deg")
print()
print("RotSkyPos when RotTelPos ~ 0, q ~ 0")
print(rtp_to_rsp(0.0, ra, dec, mjd), " deg")
print("expect ~ -90 deg")
print()
print("RotSkyPos when RotTelPos ~ 45, q ~ 0")
print(rtp_to_rsp(45.0, ra, dec, mjd), " deg")
print("expect ~ -135 deg")
print()
mjd2 = 61976.03248
print("RotSkyPos when RotTelPos ~ 0, q ~ 45")
print(rtp_to_rsp(0.0, ra, dec, mjd2), " deg")
print("expect ~ -45 deg")
print()
It yields:
pseudo parallactic angle
-0.2069151032773199 deg
expect ~0 deg
parallactic angle from astroplan
0.28310081072723475 deg
expect ~0 deg
RotSkyPos when RotTelPos ~ 0, q ~ 0
-90.20691510327731 deg
expect ~ -90 deg
RotSkyPos when RotTelPos ~ 45, q ~ 0
-135.2069151032773 deg
expect ~ -135 deg
RotSkyPos when RotTelPos ~ 0, q ~ 45
-40.95945312926989 deg
expect ~ -45 deg